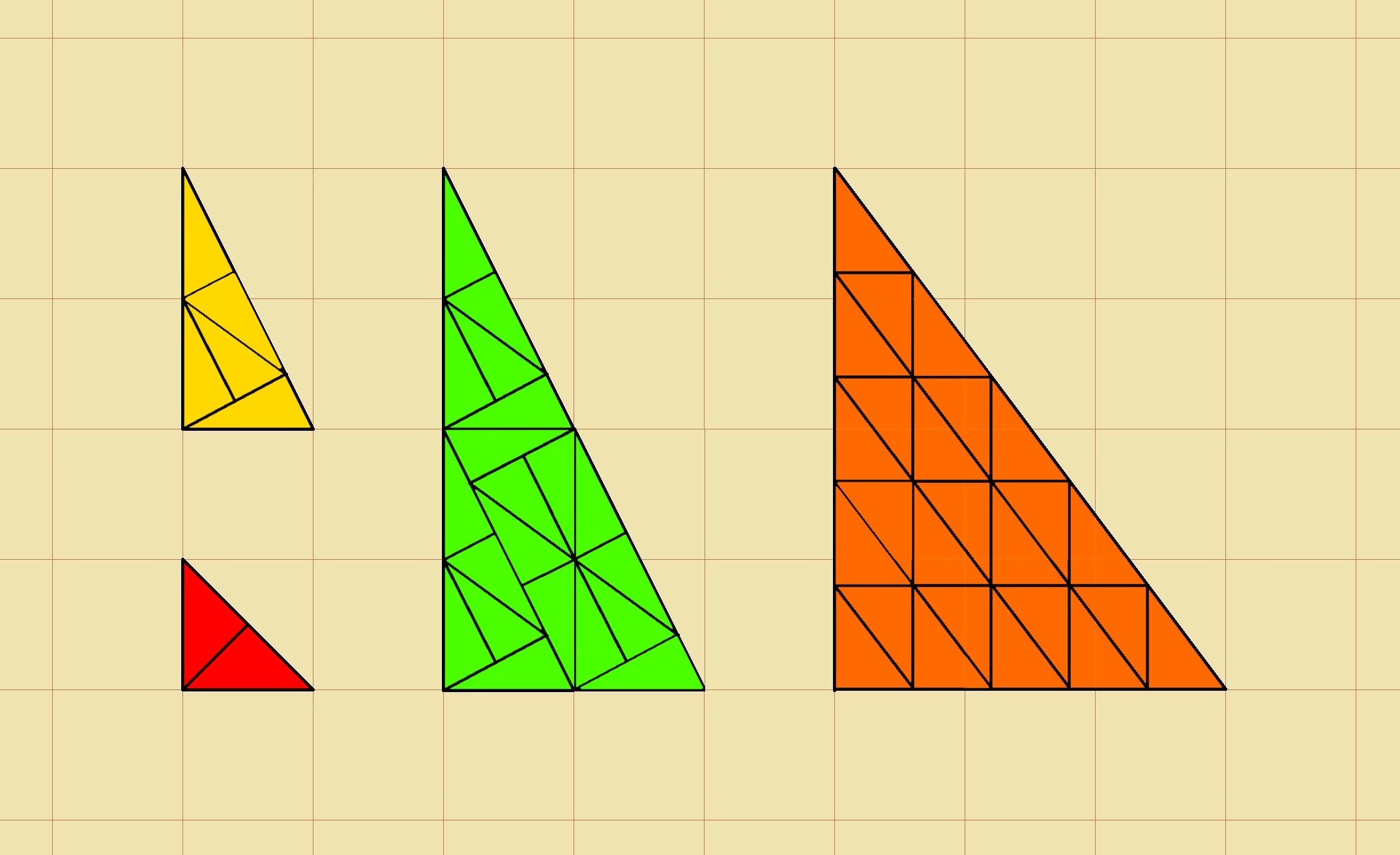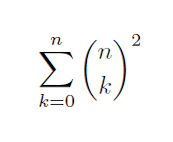Math Puzzles and Conjectures

This actually happened to me, although I have rounded the odometer reading for easier calculation. The salesman might be surprised to learn that there is enough information to solve the problem.

I bought a ten-year-old car with 200000 km on the odometer. The salesman assured me that the only previous owner was a little old lady who only used it to drive to church on Sunday. Approximately how far did she live from the church?
Answer = approximately 200 km.

This is something that happens often, but are the participants giving it enough thought?

One person thinks of a number between 1 and 10. Two others guess the number, and the closest one wins. Is there a strategy?

The answer to this problem seems unintuitively large.

In a jigsaw puzzle that is 40 by 25 pieces, what percentage of the pieces are border pieces?
Answer = 12.6%, more than one eighth of the puzzle.

This is one of the questions I submitted to Humanity's Last Exam, a benchmark designed to challenge large language models. It was rejected on the grounds that it is too easy, but the LLM solution was quite complicated.

Consider sequences of coin tosses such that:
1. The first toss is a head.
2. There are never three heads in a row.
3. There are never three tails in a row.
How many such sequences are there of length N?
Conjecture: There is a human who can find a clear answer.

In "The Puzzle Universe" (highly recommended), Moscovich remarks, "Only the Golden Triangle has the property that it can be created from five smaller copies of itself." The following is a possible generalization.

Conjecture: Let T be a right triangle with integer legs m and n. Then T has the property that it can be created from m ² + n ² smaller copies of itself.

This is a nice interview question for a candidate who claims to understand combinatorics.

Simplify:

The stripes have equal thickness. The problem is to find the area of the red stripes, given the area of the blue stripes. A solution is presented on MindYourDecisions (highly recommended).

Find a simpler solution by using a rotated copy of the figure. Answer = 116.

Four objects in a straight line have relative velocities u, v and w. The relative velocity of the first and last is
(u + v) + w     or     u + (v + w).
It doesn't matter since addition is associative.

But Einstein said to add velocities differently.

Is Einstein's addition associative?

< Return to home page.